Ante los resultados de las más recientes pruebas excale y pisa—una demostración más del pobre desempeño del sistema educativo mexicano—, el autor analiza las causas del problema, todas ellas evidentes pero a la vez ignoradas sistemáticamente.
Los directores que no pueden
medir lo que quieren,
con frecuencia quieren conformarse
con lo que pueden medir.
Russ Ackoff
Nuestro nivel en matemáticas
Mucho decimos que estamos mal en matemáticas, pero ¿por qué lo decimos? ¿Qué tan mal estamos? ¿Mal con respecto a qué o a quiénes?
En la educación, como en casi todas las disciplinas, siempre es necesario conocer el sustento o las bases sobre los cuales se construyen las afirmaciones; con ello podremos realizar mejores análisis y emitir juicios adecuados.
Precisamente, uno de los objetivos de tantas evaluaciones estandarizadas, que se aplican en México y en todo el mundo es ése, el de dar información sobre cómo estamos en comparación con lo que deberíamos saber y con lo que otros saben. Desde esta perspectiva y para poder sustentar cómo estamos en los conocimientos de matemáticas en nuestro país, analizaremos dos de las evaluaciones estandarizadas, elaboradas por muchos especialistas en la materia y que se aplican e interpretan con cuidado y profesionalismo. Éstas son los Exámenes de Calidad y el Logro Educativos (excale) del Instituto Nacional para la Evaluación de la Educación (inee) y la del Programme for International Student Assessment (pisa) de la Organización para la Cooperación y el Desarrollo Económico (ocde).
EXCALE
En los Indicadores del Sistema Educativo Nacional se establece que los alumnos que obtienen un nivel de logro “insuficiente” en los excale “tienen carencias importantes en el dominio curricular de los conocimientos, habilidades y destrezas escolares, las cuales se traducen en una limitación para poder seguir progresando satisfactoriamente en las asignaturas evaluadas”.
Como se puede observar, esta evaluación está alineada con los contenidos del programa de estudios oficial mexicano.
Presento aquí los resultados de los estudiantes con nivel de logro “insuficiente” en matemáticas (ver Tabla 1).
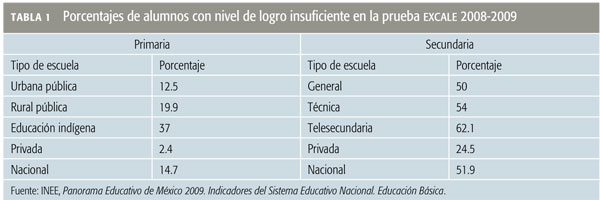
Destaca el hecho de que a nivel nacional, en primaria, 14.7% de los estudiantes no cuenta con los conocimientos necesarios para seguir estudiando matemáticas; en la secundaria la cifra es impresionante ya que cerca de 52% de los estudiantes se ubica en el nivel de “insuficiente”.
Con esta información las autoridades educativas se pueden hacer algunas preguntas y con sus respuestas establecer estrategias para corregir los problemas. Por ejemplo: ¿por qué existe una gran diferencia entre las escuelas primarias públicas y privadas? ¿Qué genera tal diferencia: los contenidos, los docentes, la cantidad de horas clase, la preparación de los docentes? Contestar estas preguntas permitiría definir las estrategias para mejorar la educación primaria y sobre todo hacerla más justa: si la educación pública es de menor calidad que la privada, se está abriendo más la brecha entre las clases sociales, pues sólo quienes pueden pagar una escuela privada tendrán acceso a educación de calidad.
Es inaceptable que en secundaria cerca de 52% de los estudiantes no tenga los conocimientos básicos para poder seguir aprendiendo. ¿Qué futuro nos espera, cuando México es un país de jóvenes?
PISA 2009
En la evaluación pisa, aplicada en 2009, se establece que el nivel 2 implica “contar con los conocimientos mínimos necesarios para que un joven pueda seguir estudiando en niveles educativos superiores o que pueda integrarse con éxito en el mercado laboral”.1 Esto implica que quien no se encuentre en este nivel, tendrá graves problemas para seguir aprendiendo.

pisa es un examen estandarizado que se aplica a una muestra de alumnos de 15 años 3 meses a 16 años de edad. En ese año, en México se aplicó en los tipos de escuelas y niveles educativos que se muestran en la Tabla 2.

Casi 73% de los evaluados se encuentra en el nivel de educación media superior. De todos los entrevistados, sólo 5.3% provenía de telesecundarias, no obstante que 21% de la matrícula de secundaria se encuentra dentro de esa modalidad y 51% en secundarias generales.2
Una de las ventajas de la evaluación pisa es que el examen y la metodología de aplicación son iguales en todos lo países donde se realiza, lo que implica que los sesgos e inconsistencias son los mismos. Esto nos permite compararnos con otros países que, nos guste o no, son nuestros competidores en la economía global.
En la Tabla 3 presento los resultados de matemáticas de algunos países, producto de la prueba pisa aplicada en 2009. En esta tabla se incluyen los resultados por niveles y por porcentaje con respecto a Shanghai-China, lugar que obtuvo el máximo nivel en los resultados; se incluyen también los resultados de Canadá y Estados Unidos, nuestros socios comerciales del norte, y los de algunos países latinoamericanos, con quienes podemos compararnos por nuestro nivel económico y cultural. Si se desea mayor información se recomienda consultar la página del inee (www.inee.edu.mx).
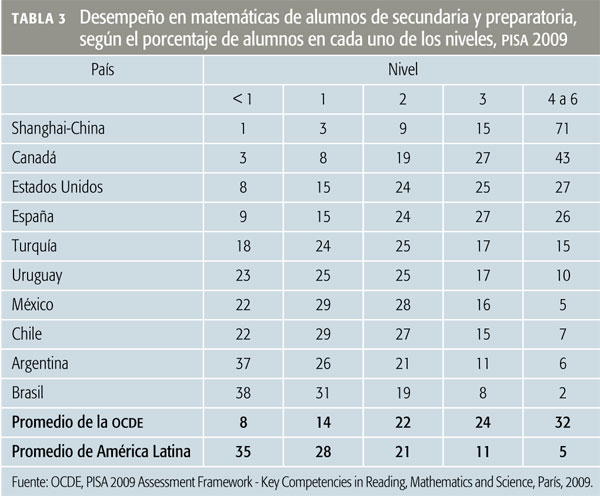
Lo primero que podemos observar es que 51% (22 + 29%) de los alumnos mexicanos que presentaron el examen está por debajo del nivel 2, hecho que nos indica que esta proporción no cuenta con los conocimientos mínimos necesarios para seguir estudiando o para integrarse al mercado laboral con éxito. Triste realidad.
No obstante que las pruebas pisa y excale no tienen relación, ya que sus metodologías de elaboración y la aplicación e interpretación son totalmente diferentes, las dos evaluaciones dan resultados similares para los niveles bajos. Más de 50% de nuestros estudiantes de secundaria o de primero de bachillerato se encuentran en los últimos niveles de las escalas de evaluación.
Si nos comparamos con otros países, nos damos cuenta de que estamos muy lejos de la excelencia de China, pues mientras este país concentra al 71% de sus alumnos en los niveles 4 a 6, en México sólo tenemos 5% en esos niveles. Con relación a nuestros socios comerciales, nos ubicamos como los menos favorecidos, pues mientras Canadá y Estados Unidos tienen 70 y 52% respectivamente en los niveles 4 a 6, México sólo tiene 5 por ciento.
Con respecto a los países hermanos de Latinoamérica, ocupamos un honroso segundo lugar. Uruguay tiene el primero, aunque habría sido inferior si Cuba hubiera participado. Estamos por arriba de la media de los países de Latinoamérica, pero en matemáticas y en la educación en general no podemos ocultar la realidad: estamos muy por debajo de los niveles que pueden lograr nuestros estudiantes.
Las causas de nuestras deficiencias en matemáticas
El asunto es multifactorial: no se puede reducir el problema a una sola causa, ni tampoco tratarlo de manera dispersa atacando de forma aislada los motivos. Es necesario buscar soluciones integrales que incluyan todos los elementos que nos han llevado a estos niveles de incompetencia matemática y plantear soluciones que ataquen todas las causas y los efectos que cada una de ellas genera en los otros elementos. Menciono que hemos llegado a estos niveles porque no debe olvidarse que durante más de 100 años, los egresados de primaria, secundaria, bachillerato y licenciatura de nuestro país han subsistido con los conocimientos matemáticos necesarios para construir un país que tiene logros importantes en ciencias sociales, ingeniería, química y otros muchos campos.
Considero que nuestro bajo nivel en matemáticas se debe a lo siguiente:
- Hemos saturado los contenidos de primaria y secundaria con conocimientos que impiden a los alumnos aprender lo esencial;
- Se arrastra un déficit de conocimiento matemático en todos los niveles de estudio, lo que implica retrasar al grupo o dejar atrás a los que no saben;
- No hemos preparado a los docentes para que dominen los temas de matemáticas que enseñan;
- No impulsamos ni dejamos a los docentes diseñar las estrategias de enseñanza necesarias para sus estudiantes;
- No a todos los temas de matemáticas les encontramos uso y por ello los olvidamos;
- Las matemáticas están rodeadas de mitos y se ha vuelto complicado enseñarlas.
Como puede observarse, estas causas tienen relación con los programas de estudio, la preparación de los docentes, la carencia de libertad para que los profesores enseñen como lo necesitan sus alumnos, el uso de las matemáticas en la vida diaria y la cultura matemática de nuestra nación.
Los niños y jóvenes mexicanos, como todos los del mundo, tienen las mismas necesidades, motivos y capacidades para aprender matemáticas, nosotros (padres, maestros y educadores) somos los que durante su desarrollo les ayudamos a “alambrar” su cerebro de diferentes maneras y cuando lo necesitan no hacen otra cosa que usar su mente como les enseñamos.
El hecho de no poder lograr que los niños y jóvenes de un país aprendan matemáticas significa privarlos de la posibilidad de reflexionar para tomar decisiones, anticiparse a lo que puede suceder, afirmar con certeza, aprender a aprender y entender otras disciplinas. Las matemáticas, precedidas por la lectura, son la llave para acceder a todos los demás conocimientos. No podemos dejar a los niños y jóvenes de un país sin esa herramienta.
Análisis de las causas
Antes de explicar cada una de las causas expuestas, es necesario mencionar un elemento que impacta en el aprendizaje no sólo de las matemáticas sino de todas las materias. En primero de primaria se proporciona a los niños seis libros para que estudien sus contenidos, entre ellos los de matemáticas y de recortables. Pero resulta que los niños aún no saben leer, hecho que les impide el uso de dichos libros e impone una carga extra al docente.
1. Exceso de contenidos que impide el aprendizaje de lo esencial
En cada reforma o actualización educativa se agregan a los contenidos de primaria y secundaria temas de estudio y lecciones, mientras que las horas para su tratamiento son las mismas. Parece ser que quienes diseñan dichos contenidos no toman en consideración que los docentes tienen que atender a niños desnutridos, maltratados, con deficiencias en los conocimientos previos y que, además, deben estudiar otras cinco o siete materias. En los libros de matemáticas de primaria se deben analizar, en promedio, 50 lecciones por grado, y en los de secundaria 30. Si tenemos en cuenta que en muy pocas ocasiones logramos 200 días de clases por ciclo escolar y que se deben estudiar otras materias, debería darse prioridad a lo primero, sin permitir que ningún niño o joven se quede sin los conocimientos básicos de matemáticas y álgebra. Debemos recordar que no existe la reprobación en primaria, hecho que produce egresados a granel pero sin calidad en sus conocimientos. Es preferible dar pocos temas bien aprendidos, a muchos temas a medias. Los conocimientos básicos son los que permiten seguir estudiando las matemáticas, por ejemplo conocer las operaciones básicas con enteros, decimales y fracciones y su aplicación para plantear y resolver problemas prácticos, en resumidas cuentas la aritmética. Una vez que se domine esto, se puede enseñar lo que se quiera sin límites. Más aun, el estudiante buscará por sí solo cómo aprender más. No debería haber un solo niño o joven con educación básica que no cuente con la habilidad de resolver problemas relacionados con las operaciones básicas y el álgebra. Claro que estas operaciones básicas se pueden aprender con geometría, medición y representación de la información. Pero el principal objetivo de estudio en la primaria debe ser el conocimiento y aplicación de las operaciones básicas y no los otros agregados.
2. Se arrastra un déficit de conocimiento matemático en todos los grados
El que los alumnos lleguen mal preparados, como se dice en el argot de las aulas, es grave para ellos mismos, para el profesor y desde luego para la escuela. Este problema es producto del exceso de contenidos y la velocidad con la que los profesores deben tratar el cúmulo de lecciones del ciclo escolar. Si ya se sabe que los alumnos no inician los ciclos escolares con los conocimientos suficientes para abordar nuevos temas, ¿por qué no se incluye en el plan de estudios un tiempo para regularización y confirmación de conocimientos?
El déficit se incrementa año con año pues, con tanta lección, se tienen que tratar a vuelo de pájaro los conceptos que deben aprenderse a profundidad. Sólo los alumnos que cuentan con las bases siguen al profesor; los demás hacen como que aprenden, al fin van a acreditar. Éste es un problema exponencial ya que, conforme avanza, las lagunas del alumno son mayores, a tal grado que en ocasiones los estudiantes de bachillerato no saben sumar, restar o dividir fracciones, mucho menos plantear la solución a un problema por medio de una ecuación o sacar un porcentaje.
Cada profesor tendría que contar con una guía de los conocimientos mínimos que requieren los alumnos para poder aprender lo programado en el grado correspondiente, y seguir adelante sólo hasta que los alumnos cuenten con esos conocimientos. Esto parece difícil, pero con menos contenidos y la voluntad del docente se puede hacer.
3. No hemos preparado a los docentes para que dominen los temas de matemáticas que enseñan
Que los temas de matemáticas sean elementales no implica que no tengan dificultad. Tratemos de definir, por ejemplo, qué es la numeración y cómo es que ésta se logra. El lector se dará cuenta de que no es fácil dar una respuesta, aunque usamos la numeración todos los días. Éste es el tipo de retos que enfrentan los docentes de primaria y secundaria. Por ello los profesores de educación básica deben ser expertos en todo lo que se refiere a las bases de la aritmética y el álgebra. Sobre todo deben conocer los problemas para el aprendizaje de dichas bases. No podemos enseñar lo que no conocemos. Una forma para lograr lo anterior es proporcionar a los docentes muchos ejemplos de la aplicación de los conocimientos matemáticos que van a enseñar. Puede hacerse por medio de boletines de divulgación y de recomendaciones pedagógicas. Hay que evitar que estos boletines sean acartonados y que empleen la jerga de las ciencias de la educación. Es importante diseñar una gran cantidad de estrategias de enseñanza de cada uno de los temas base y que los docentes tengan acceso a todas ellas. También es necesario que los docentes recurran a sitios de internet actualizados donde sea posible practicar lo que se enseña. Los profesores comprometidos con su carrera de inmediato asimilarán las propuestas e incluso propondrán muchas otras.
Además de lo anterior, es necesario que nuestros profesores se preparen de manera constante y que se certifiquen por lo menos cada dos años a través de un organismo externo a la sep, como se hace en la mayoría de los países con buenos resultados. No pueden seguir dando clases de matemáticas aquellos docentes que no estén capacitados para ayudar a los alumnos a aprender la materia.
4. No dejamos a los docentes diseñar las estrategias de enseñanza necesarias para sus estudiantes
En los últimos años se han diseñado los contenidos para el aprendizaje de las matemáticas por medio de lecciones en las que se establece, de manera precisa y religiosa, lo que se pretende que los alumnos aprendan. Además, se ha utilizado casi siempre el método de aprendizaje por descubrimiento para que los alumnos construyan su conocimiento. Ambos elementos pueden funcionar de manera adecuada pero no de manera universal pues la diversidad de estilos de aprendizaje de los alumnos es muy grande. Desde mi punto de vista, meten al docente en una carretera sin retornos y de un solo carril. El maestro no puede rebasar y además no le enseñaron a conducir el vehículo con el que recorre dicha carretera. El desastre se da porque debe seguir un solo método que no domina.
Dada la gran diversidad de nuestros alumnos, el docente debe tener entre sus habilidades la capacidad de crear nuevas formas de enseñar. Éstas deben lograr atrapar la atención y el entusiasmo de los alumnos: que éstos se identifiquen con él como su amigo, facilitador, profe o como se le quiera llamar. Lo importante es que lo reconozcan como el que los ayuda y guía. Ello permitirá a los docentes retomar el lugar social que les corresponde. El profesor debe ser tratado como un profesional con la capacidad de orientar a sus alumnos en sus procesos de aprendizaje y de crear estrategias de enseñanza cada vez que sea necesario. Si el docente considera adecuado que debe enseñar todo lo referente a las fracciones en tres lecciones y con gráficas de queso y esto le da resultado, pues se le debe permitir que diseñe su programa, en lugar de que un libro le diga qué hacer. Los libros de texto son guías de aprendizaje: no deberían ser camisas de fuerza o medios para supervisar los avances de los docentes.
Se debe depositar la confianza en los profesores y apoyarlos con mucha información; esto propiciará que logren mejores resultados. Los docentes que no consigan los resultados esperados deberán abandonar las aulas hasta que estén capacitados para la enorme responsabilidad de ayudar a sus alumnos a aprender.
5. No todos le encontramos uso a los temas de matemáticas y por ello los olvidamos
Uno de los elementos más importantes en el proceso de enseñanza-aprendizaje es que los contenidos sean útiles y significativos. Al uniformar por medio de lecciones todo lo que se debe aprender en todos los lugares de nuestro país, es muy probable que no se incluya lo que puede ser útil y significativo en las diferentes comunidades. La libertad del docente para adaptar lo que se va a aprender a la vida diaria de los alumnos tiene resultados sorprendentes, pues lo que se aprende y se practica es muy seguro que se perfeccione. Todo lo que se enseñe de matemáticas en la primaria y secundaria debe poderse aplicar en la vida cotidiana de los alumnos, lo que sólo se puede lograr por medio del ingenio y las habilidades de nuestros docentes. Una vez más sale a la luz la libertad para ejercer la profesión de maestro.
6. Los mitos en torno a las matemáticas y lo complicado que se ha vuelto enseñarlas
Padres de familia, maestros, científicos, gobernantes y alumnos califican a las matemáticas como complejas, difíciles, feas y aburridas. Además, existen personas, algunas exitosas y otras no tanto, que dicen que ellos sin saber matemáticas han vivido muy felices, que no es necesario complicarse la vida aprendiéndolas. Esto se debe al nivel de cultura matemática de nuestro país.
Las matemáticas implican voluntad, comprensión, reflexión, constancia y creatividad, lo que obliga a realizar un esfuerzo intelectual que no siempre se puede lograr en poco tiempo. No existen caminos mágicos para aprender matemáticas al vapor: su conocimiento se obtiene con tiempo y práctica, elementos que no siempre están considerados en los planes de estudio ya que se debe ver todo en un plazo determinado y con lecciones preestablecidas.
Es mentira que las matemáticas sólo sean para los inteligentes. Todos nacemos con las capacidades para aprender las matemáticas y además todos hacemos matemáticas en nuestra vida. Unos las aprenden más rápido que otros, sólo es cuestión de tiempo y de tener las bases para entenderlas. El tiempo es para reflexionar y las bases son para construir sobre lo que ya se sabe.
Los problemas son varios y todos están ligados: no se puede tratar uno sin tomar en consideración los demás. No se puede cambiar el nivel de las matemáticas de nuestro país sin la intervención de los docentes, pero no sólo se debe trabajar con los docentes sino también con todo lo que implica su práctica profesional.
Es muy importante destacar que mejorar en matemáticas no implica sólo que nuestros alumnos sepan resolver problemas usando números y operaciones artiméticas. Lo que en realidad se pretende es que ellos cuenten con las bases para seguir aprendiendo ésta y otras muchas materias.
Cómo enseñar las matemáticas
La enseñanza de las matemáticas se ha complicado en la era del conocimiento. Al mismo tiempo, se recurre poco a la información y las herramientas que están al alcance de casi todos en internet para enseñar esta materia. No se usan los miles de ejercicios y programas de matemáticas que existen para practicar lo que se aprende en la escuela. Usarlos haría más fácil y divertido entender los conceptos y ejercitarse. Pero, ¿cómo se van a utilizar si no se incluyen en las lecciones que hay que seguir de manera militar?
La enseñanza de las matemáticas no debe ser tan compleja. Si tenemos en consideración lo que varios cognotivistas señalan, podríamos concluir que no se debe ir en contra de la naturaleza de los estudiantes, por lo que nuestros métodos de enseñanza deben tener en consideración las características de las edades de los alumnos:
• A los niños se les enseña con el juego;
• A los jóvenes, por medio de la participación en grupo y con retos;
• A los adultos, por medio de la aplicación de los conocimientos para obtener otros nuevos.
Se dice que la construcción del conocimiento se da en el ser humano por alguna de las siguientes razones:
- Por la necesidad de solucionar un problema importante para subsistir o lograr una meta. La necesidad es la madre de las ciencias;
- Porque no encuentra una explicación a un hecho que le interesa o impresiona. Por ejemplo, un fenómeno natural al que no se le encuentra explicación. El ser humano es curioso y por ello investiga y ha logrado un grado de desarrollo;
- Porque sus semejantes le indican lo que puede aprender. El instinto de conservación nos obliga a seguir la orientación de los padres y posteriormente el alumno se somete a los estudios en una escuela;
- Porque se da cuenta de que no sabe y necesita aprender para ser como los demás. El aprendizaje de tipo social nos permite relacionarnos con quienes nos rodean;
- Por el placer de aprender. El hombre por sí solo se acerca al aprendizaje, que está en relación con los conocimientos previos. Por ello es que siempre se debe estar aprendiendo
Como puede verse, los hechos que influyen en el aprendizaje de los individuos no están alejados de la escala de desarrollo de Maslow.3 El problema es que en muchas ocasiones sólo está actuando la tercera causa —que otros nos digan lo que debemos aprender—, cuando el aprendizaje más natural requiere la convergencia de las cinco.
En el caso concreto de la enseñanza de las matemáticas, la experiencia indica que a lo anterior hay que agregar tres o cuatro elementos.
Práctica, práctica, práctica y práctica
Sin que sea la panacea, un método que siempre da buenos resultados para el estudio de las matemáticas es el del aprendizaje por medio de la solución de problemas. A continuación menciono algunos elementos que caracterizan a este método:
- Si se comprende el problema se obtiene un grado importante de asimilación, pues el alumno estará consciente del reto al que se enfrenta;
- Cuando se entiende el problema, éste se vuelve significativo para el alumno;
- Al enfrentar un problema matemático, se echa a volar la imaginación para resolverlo, lo que implica investigar, reflexionar, descubrir y probar, actividades que dan satisfacción al ser humano y, desde luego, aumentan su conocimiento;
- Para encontrar la solución, se hace un análisis profundo de los diferentes elementos matemáticos que se requieren, hecho que implica recordar, aprender y actuar con seguridad;
- Los elementos matemáticos necesarios para la solución no se obtienen de la memoria: se vuelven a descubrir, lo que implica reflexión;
- Obliga a pensar, lo que implica hacer que nuestro cerebro ponga en marcha mecanismos que lo alertan y le ayudan para adquirir habilidades para el uso de las matemáticas en la solución de problemas;
- Entre más intentos de solución, más se aprende, ya que cada vez que se plantea una alternativa se estará reflexionando sobre lo que funciona y lo que no;
- Un problema puede resolverse por diferentes procedimientos, lo que implica diversidad de razonamientos para llegar a un mismo fin;
- El tomar un reto matemático y encontrar su solución implica satisfacción, lo que hace que se busquen nuevos retos y con cada uno se adquiera más experiencia.
La técnica de la enseñanza de las matemáticas por medio de problemas fue la primera que utilizó la humanidad. Existe evidencia en la forma como se enseñaban los cálculos para construir las pirámides y en el trazo de canales de riego mostrado en el papiro de Rhind, descubierto en Tebas por el egiptólogo Alexander Henry Rhind hacia el año de 1858. El pergamino fue elaborado por el sacerdote Ahmes (1680-1620 a.C.). En él se plasman métodos de cálculo por medio de 85 problemas relacionados con el uso de fracciones, la solución de ecuaciones, progresiones y series, y el cálculo de áreas y volúmenes.
En la actualidad, se tienen varias referencias documentadas sobre el aprendizaje por medio de problemas, como la de Learning Based Problems de 1960, registrada por la Universidad de McMaster de Hamilton en Canadá; posteriormente fue ampliamente utilizada en las universidades de Queen Mary, Maastrich y Aalborg.
No debemos olvidar los cuadernos Gader, la serie de matemáticas y geometría Schaum y el libro propedéutico para el bachillerato de la educación para adultos del inea. Todos ellos se fundamentan en el desarrollo y tratamiento de problemas.
La técnica de aprendizaje por medio de la solución de problemas está por demás probada. Parte de las teorías educativas de Vygostsky y Dewey. El verdadero intríngulis de la técnica se encuentra en la selección de los problemas y la manera en la que éstos se presentan a los alumnos. Todas las virtudes de esta técnica se pueden volver en contra del docente si esos elementos no se tienen en cuenta.
Para lograr el aprendizaje con esta técnica, no sólo se debe arrojar un problema a los alumnos y que lo resuelvan: hay que seguir una estrategia preestablecida. Doy el siguiente ejemplo:
- Presentación del tema por medio de la solución y entendimiento de un problema. Esto implica primero explicar un tema por medio de la solución de un problema y después recurrir a las bases teóricas;
- Planteamiento a los alumnos de uno o varios problemas relacionados con el tema a aprender. El docente debe estar seguro de que los alumnos entienden los problemas, y además formar equipos para que se busquen las soluciones;
- Discusión en los equipos de las posibles soluciones y posiciones de los alumnos;
- Reflexión de los alumnos en equipo sobre las posibles soluciones del problema o búsqueda de herramientas matemáticas para acercarse a la solución. El docente puede orientar sobre las herramientas matemáticas;
- Planteamiento y desarrollo de la solución;
- Exposición y discusión ante el grupo de las soluciones obtenidas en los equipos de trabajo;
- Comprobación y comparación de los resultados obtenidos.
Desde luego, todo esto parte de un objetivo de aprendizaje y un muy buen problema. Uno de los mayores inconvenientes de esta técnica es que requiere de tiempo del docente para preparar y conducir la clase, tiempo con el que no siempre se cuenta. Sin embargo, sus resultados son sorprendentes.
A manera de cierre, me permito destacar que un grave error sería preparar a los alumnos de la educación básica para obtener mejores puntuaciones en las pruebas estandarizadas. Lo que nuestro país necesita son niños y jóvenes pensantes y reflexivos, que sepan cómo utilizar las matemáticas para la toma de decisiones en su vida diaria. Con ello se podrá construir un México con un futuro mejor.
ALFONSO RAMÓN BAGUR es Director del Fondo Mexicano para la Educación y el Desarrollo e investigador externo del Instituto de Ingeniería de la
unam.
_________________________________
1 inee, Pisa en México 2009, p. 38-39.
2 sep, Sistema Educativo de los Estados Unidos Mexicanos: principales cifras del ciclo escolar 2007-2008.
3 Abraham Maslow, El hombre autorrealizado. Hacia una psicología del ser, Cairós, España, 2009.







Me llamo Enrique Barcelona, soy licenciado en Matemáticas cubano y radico en México. En mi experiencia de 26 años de trabajo como profesor de Matemáticas en el nivel de preparatoria y secundaria , he reconocido la necesidad de revertir la situación actual aqui en jalisco a través de la creación de talleres impartidos tanto a alumnos como a maestros para el dominio de la materia. No es nada difícil lograr este objetivo si contara con el apoyo de una organización tan prestigiosa. Espero su respuesta.
osea que si el que invento las matematicas se tiro de hocico por un barranco nosotros tambien nos vamos a tirar, yo creo que ese wey no tenia nada que hacer.
Muchos de nuestros niños de primaria y hasta de nivel secundaria tienen dificultade con el pensamiento matemático, hay quienes no dominan las tablas de multiplicar y las operaciones básicas, por lo tanto su brecha para el cálculo mental es notoria. Como observador de esta problemática, En el canal de youtube «Aprendizaje Universal» presentaré algunos videos de niños pequeños ejecutando ecuaciones algebráicas o mostrando algunas habilidades de pensamiento matemático. Pero si nuestro gusto por leer es casi nulo ¿Nos interesarán las matemáticas?
Me parece muy interesante su artículo, si desde niños nos enseñaran las mateamáticas con juegos y paciencia y nuestros profesores tuvieran el amor a las matemáticas otra cosa sería, en lo particular después de 12 años de haber llevado matemáticas Financieras, y retomar el estudio de estas con la ayuda de un excelente Mtro. estoy aprendiendo nuevamente Matemáticas las cuales habían sido una pesadilla y en este momento que las entiendo me parecen maravillosas
Con estas palabras de ayuda, pienso que nuestros alumnos trabajaran con mas interes y claro los docentes que debemos formarnos en la lectura critica y reflexiva. Excelente ensayo, gracias por la aportacion.